有限差分法及matlab实现

发布于 2024-10-20  353 次阅读

AI 摘要

本文介绍了有限差分法在求解微分方程中的应用，以及应用MATLAB实现有限差分法的示例代码。有限差分法是一种数值方法，常用于工程仿真模拟等领域。文章通过推导泰勒公式展开得到一阶和二阶微分的中心差分公式，并展示了如何用MATLAB编写求解常见偏微分方程的数值解的代码。代码中包括了划分网格、组建系数矩阵、差分求解以及误差分析等步骤，最后展示了有限差分法得出的数值解与解析解之间的误差分析。文章还提及了二者间的截断误差满足二阶精度要求。

有限差分法是一种求解微分方程的数值方法，它仅为一种数学上的逼近，在物理意义上并无实际含义。随着计算机技术的快速发展，有限差分法成为了一种非常有效的计算手段，在工程仿真模拟（如FLAC 3D等软件）中有大量应用。（话说这学期又被逼着速成FLAC了，回想起了上学期Plaxis的恐惧QAQ）

(1)   \begin{equation*} u(x+h)=u(x)+hu'(x)+\dfrac{h^2}{2}u''(x)+\dfrac{h^3}{6}u^{(3)}(x) +\dfrac{h^4}{12}u^{(4)}(x+\xi)} \end{equation*}

其中\xi\in(0,h)

从上面的公式不难看出，当h足够小时，等式右端的前几项将近似等于左端，这就是泰勒公式“逼近”的思想。

将左端的式子表达式泰勒展开，进而可以得到如下的差分公式：

向前差分（一阶）

(2)   \begin{equation*}u'(x)=\dfrac{u(x+h)-u(x)}{h}-\dfrac{h}{2}u''(x+\xi) \end{equation*}

向后差分（一阶）

(3)   \begin{equation*}u'(x)=\dfrac{u(x)-u(x-h)}{h}+\dfrac{h}{2}u''(x+\xi) \end{equation*}

中心差分（一阶）

(4)   \begin{equation*}u'(x)=\dfrac{u(x+h)-u(x-h)}{2h}-\dfrac{h^2}{6}u^{(3)}(x+\xi)\end{equation*}

向前向后差分具有一阶近似精度，而中心差分则具有二阶近似精度，三者计算量差距不大，因此通常采用中心差分格式。

类似地，将u(x+h)继续展开,可以得到二阶微分的中心差分公式：

(5)   \begin{equation*}\dfrac{u''(x)=u(x+h)-2u(x)+u(x-h)}{h^2}-\dfrac{h^2}{12}u^{(4)}(x+\xi)\end{equation*}

应用上述差分方法可以求出常见偏微分方程的数值解，比如下面的例题

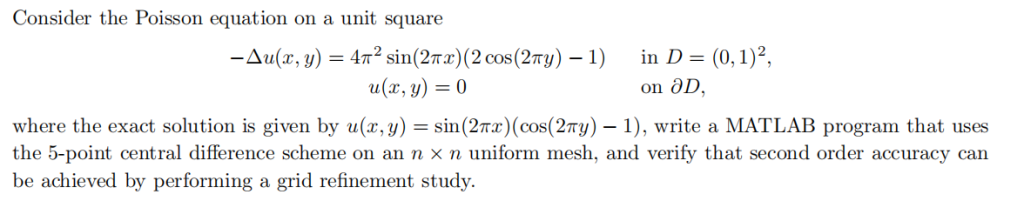
使用MATLAB编写的求解代码如下：

%Problem 5
clear;clc;

% --------------------------划分网格--------------------------------------
for k=1:10
    n=10*k-1;%网格内点数（（n+1）×（n+1））
    a=0;b=1;c=0;d=1;%网格划分区域
    h=(b-a)/(n+1);%步长
    x(1)=a;x(n+2)=b;%定义x轴边界点坐标
    y(1)=c;y(n+2)=d;%定义y轴边界点坐标
    for i=2:n+1
        x(i)=a+(i-1)*h;
    end %定义x轴内网格点坐标
    for j=2:n+1
        y(j)=c+(j-1)*h;
    end %定义y轴内网格点坐标

% -------------------------组建系数矩阵------------------------------------

    B=diag(4*ones(1,n))+diag(-ones(1,n-1),1)+diag(-ones(1,n-1),-1);
    I=-eye(n);
    A=kron(diag(ones((n-1),1),-1),I)+kron(diag(ones((n-1),1),1),I)+kron(diag(ones(1,n)),B);
    A=A/h.^2;
   
% ----------------------------差分求解-------------------------------------
    f=zeros(n,n);
    for i=1:n %y
        for j=1:n %x
            f(i,j)=4*pi.^2*sin(2*pi*j*h)*(2*cos(2*pi*i*h)-1);
        end
    end%求网格上点对应的函数值
    f=f';
    f=f(:);
    u1=A\f;
    u1=reshape(u1,n,n)';
    u=zeros(n+2,n+2);
    for i=2:n+1 %y
        for j=2:n+1 %x
            u(i,j)=u1(i-1,j-1);
        end
    end
    % disp(u);
    U=zeros(n+2,n+2);
    for i=2:n+1 %y
        for j=2:n+1 %x
            U(i,j)=sin(2*pi*(j-1)*h)*(cos(2*pi*(i-1)*h)-1);
        end
    end  
    % disp(U);
% ----------------------------------误差分析------------------------------
    dif(k)=0;
    for i=1:n+2
        for j=1:n+2
            if dif(k)<abs(U(i,j)-u(i,j))
                dif(k)=abs(U(i,j)-u(i,j));
            end
        end
    end
end
beta1 = log2((dif(1)-dif(2))/(dif(2)-dif(4)))
beta2 = log2((dif(2)-dif(4))/(dif(4)-dif(8)))
% ------------------------------------绘图---------------------------------
% [m_x,m_y]=meshgrid(x,y);
% u_z=u;
% U_z=U;
% mesh(m_x,m_y,u_z,'edgecolor','r','linewidth',0.1);
% hold on;
% mesh(m_x,m_y,U_z,'edgecolor','b','linewidth',2.5);
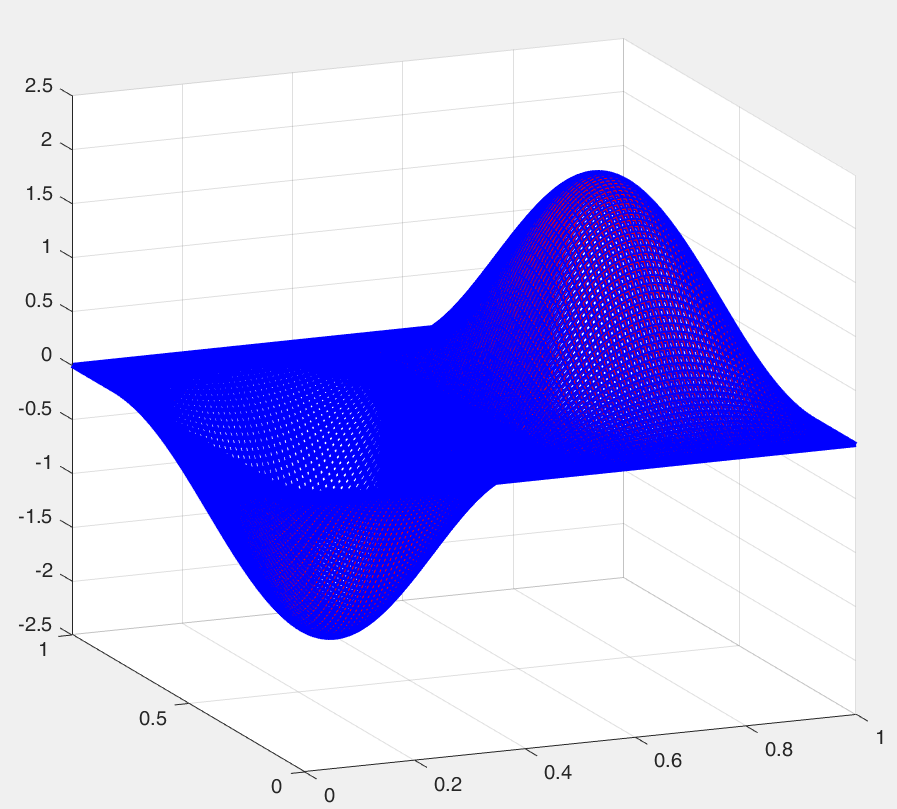
% hold off;%绘图

有限差分法得出的数值解和解析解如下图所示，二者间的截断误差满足二阶精度要求