算法原理
从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径叫做最优路径,解决该问题的方法包括Dijkstra算法、Bellman-Ford算法、Floyd算法和SPFA算法等。
Dijkstra 算法,是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年发现的算法,戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。Dijkstra 算法原始版本仅适用于找到两个顶点之间的最短路径,后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径,产生一个最短路径树。本算法每次取出未访问结点中距离最小的,用该结点更新其他结点的距离。需要注意的是绝大多数的Dijkstra 算法不能有效处理带有负权边的图。
Dijkstra算法的思路:
- 算法初始,将选择的源点
 放进集合
放进集合













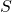
- 无自环的源点












- 当顶点






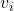














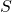














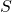












- 将源点


















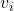
![Rendered by QuickLaTeX.com dist[s,v_i]](https://tuanyuan-1305620998.cos.ap-shanghai.myqcloud.com/puff-load.svg)
![Rendered by QuickLaTeX.com dist[s,v_i]](https://tuanyuan.xyz/wp-content/ql-cache/quicklatex.com-4ba85dd297d2db23f70bd5ee4f3e9cc6_l3.png)


























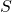
![Rendered by QuickLaTeX.com dist[s,v_i]=\infty](https://tuanyuan-1305620998.cos.ap-shanghai.myqcloud.com/puff-load.svg)
![Rendered by QuickLaTeX.com dist[s,v_i]=\infty](https://tuanyuan.xyz/wp-content/ql-cache/quicklatex.com-e19d0af63d098ae8c1be3b82fa5e222c_l3.png)


















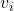












- 如果集合


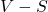
- 选出经过第一个循环后的,在集合


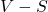














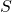








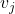
- 将这个顶点








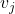














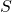














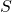
- 将顶点








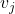














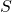














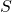




















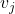














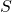








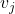








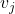


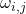


















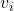














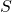


















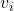














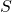




















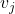














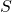








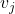






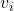


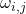
Dijkstra算法的时间复杂度是![]()
![]()
![]()
![]()
![]()
分别为赋权有向图中的顶点个数和边的个数。Dijkstra算法的时间复杂度是![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
而选择基于堆实现的优先队列数据结构,可将Dijkstra算法的时间复杂度降为![]()
![]()






Comments NOTHING